Trong lịch trình toán lớp 8 phần số học: Chương Phương Trình hết sức quan trọng. Đặc biệt kỹ năng này còn có trong đề thi kiểm soát 1 tiết, đề thi học tập kì lớp 8 và tương quan trực sau đó thi 9 vào 10 nên học sinh lớp 8 cần học thật kiên cố chắn.Dưới đây, hệ thống giáo dục trực tuyến đường Vinastudy xin ra mắt một vài lấy ví dụ về các bài toán Giải bài bác toán bằng phương pháp lập phương trình. Hi vọng tài liệu sẽ có lợi giúp những em ôn tập lại kỹ năng và rèn luyện kĩ năng làm bài. Bạn đang xem: Bài tập giải phương trình
BÀI TẬP LUYỆN TẬP
Bài 1:
Một số tự nhiên và thoải mái có nhì chữ số. Chữ số hàng đơn vị chức năng gấp cha lần chữ số sản phẩm chục. Trường hợp viết thêm chữ số 2 xen thân hai chữ số ấy thì được một vài mới to hơn số ban sơ 200 đối chọi vị. Tìm số thuở đầu ?
Bài 2:
Một số thoải mái và tự nhiên có hai chữ số. Chữ số sản phẩm chục gấp đôi lần chữ số hàng 1-1 vị. Trường hợp ta đổi khu vực chữ số hàng chục và hàng đơn vị chức năng thì được số bắt đầu kém số cũ 36 1-1 vị. Tìm số ban đầu?
Bài 3.
Một số tự nhiên và thoải mái có nhị chữ số. Tổng chữ số hàng chục và hàng đơn vị chức năng là 16. Ví như viết thêm chữ số 0 xen thân hai chữ số ấy thì được một trong những mới to hơn số ban đầu 630 1-1 vị.
Tìm số ban đầu ?
Bài 4.
Hai giá đựng sách có 320 cuốn sách. Nếu gửi 40 cuốn tự giá thứ nhất sang giá sản phẩm công nghệ hai thì số sách sinh hoạt giá lắp thêm hai sẽ thông qua số sách sinh sống giá sản phẩm nhất. Tính số sách thuở đầu ở từng giá.
Bài 5.
Một cửa hàng ngày trước tiên bán được rất nhiều hơn ngày trang bị hai 420kg gạo.Tính số gạo cửa hàng bán được trong ngày trước tiên biết ví như ngày thứ nhất bán đạt thêm 120kg gạo thì số gạo bán được sẽ bán được gấp rưỡi ngày máy hai.
Bài 6.
Tổng số dầu của hai thùng A cùng B là 125 lít. Nếu lấy sút ở thùng dầu A đi 30 lít và sản xuất thùng dầu B 10 lít thì số dầu thùng A bằng $frac34$số dầu thùng B. Tính số dầu ban sơ ở từng thùng.
Bài 7.
Giá sách đầu tiên có số sách bởi $frac34$ số sách của giá sách thứ hai. Ví như ta đưa 30 quyển sách từ giá trước tiên sang giá thiết bị hai thì số sách vào giá đầu tiên bằng $frac59$ số sách trong giá đồ vật hai. Hỏi cả hai giá đựng sách có từng nào quyển sách?
Bài 8.
Một căn vườn hình chữ nhật gồm chu vi bởi 112 m. Biết rằng nếu tăng chiều rộng lên bốn lần với chiều dài lên bố lần thì quần thể vườn vươn lên là hình vuông. Tính diện tích s của vườn ban đầu.
Bài 9.
Một hình chữ nhật tất cả chu vi bằng 114 cm. Hiểu được nếu sút chiều rộng lớn đi 5cm cùng tăng chiều nhiều năm thêm 8cm thì diện tích khu vườn không đổi. Tính diên tích hình chữ nhật.
Bài 10.
Một hình chữ nhật gồm chiều dài bởi $frac54$ chiều rộng. Giả dụ tăng chiều dài thêm 3 cm và tăng chiều rộng thêm 8 cm thì hình chữ nhật thay đổi hình vuông. Tính diện tích của hình chữ nhật lúc đầu ?
Bài 11.
Một miếng khu đất hình chữ nhật bao gồm chu vi bằng 98m. Nếu giảm chiều rộng 5m với tăng chiều dài 2m thì diện tích s giảm 101 $m^2$. Tính diện tích s mảnh đất ban sơ ?
Bài 12:
Một khu vườn hình chữ nhật bao gồm chu vi bằng 152 m. Ví như tăng chiều rộng lên tía lần với tăng chiều lâu năm lên hai lần thì chu vi của căn vườn là 368m. Tính diện tích s của vườn ban đầu.
Bài 13.
Một tín đồ đi xe hơi từ A đến B với gia tốc 35 km/h. Khi tới B người đó nghỉ ngơi 40 phút rồi trở lại A với gia tốc 30 km/h. Tính quãng con đường AB, biết thời hạn cả đi với về là 4 giờ 8 phút.
Bài 14.
Một bạn đi ô tô từ A mang đến B với tốc độ 40 km/h rồi trở lại A với vận tốc 36 km/h. Tính quãng mặt đường AB, biết thời gian đi từ bỏ A mang đến B ít hơn thời gian đi trường đoản cú B về A là 10 phút.
Bài 15.
Một xe hơi đi tự A đến B với gia tốc 40 km/h. Bên trên quãng đường từ B về A, tốc độ ô tô tạo thêm 10 km/h nên thời hạn về ngắn thêm thời gian đi là 36 phút. Tính quãng con đường từ A đến B?
Câu 16:
Một xe pháo ô tô dự định đi từ A đến B với tốc độ 48 km/h. Sau khoản thời gian đi được một giờ thì xe pháo bị hỏng phải tạm dừng sửa 15 phút. Vì vậy đến B đúng giờ dự tính ô tô buộc phải tăng tốc độ thêm 6 km/h. Tính quãng mặt đường AB ?
Câu 17:
Một ô tô phải đi quãng đường AB nhiều năm 60 km vào một thời hạn nhất định. Xe cộ đi nửa đầu quãng mặt đường với tốc độ hơn ý định 10 km/h và đi nửa sau hèn hơn dự định 6 km/h. Biết xe hơi đến đúng dự định. Tính thời hạn dự định đi quãng mặt đường AB ?
Câu 18:
Một ô tô dự định đi trường đoản cú A mang đến B với tốc độ 50km/h. Sau khoản thời gian đi được $frac23$ quãng đường với tốc độ đó, vày đường cạnh tranh đi nên người điều khiển xe buộc phải giảm gia tốc mỗi giờ 10 km trên quãng đường còn lại. Bởi đó, bạn đó cho B chậm trong vòng 30 phút so với dự định. Tính quãng mặt đường AB ?
Bài 19:
Một xe hơi đi từ hà nội đến Đền Hùng với gia tốc 30 km/h. Trên quãng đường từ thường Hùng về Hà Nội, gia tốc ô tô tạo thêm 10 km/h nên thời hạn về ngắn thêm một đoạn thời gian đi là 30 phút. Tính quãng đường tử tp hà nội đến Đền Hùng?
Bài 20:
Một fan đi xe máy ý định từ A cho B trong thời gian nhất định. Sau thời điểm đi được nửa quãng con đường với gia tốc 30 km/h thì tín đồ đó đi tiếp nửa quãng đường còn lại với gia tốc 36 km/h cho nên đến B nhanh chóng hơn dự tính 10 phút. Tính thời gian dự định đi quãng mặt đường AB ?
HƯỚNG DẪN GIẢI
Bài 1:
Một số tự nhiên có nhị chữ số. Chữ số hàng đơn vị gấp tía lần chữ số mặt hàng chục. Ví như viết thêm chữ số 2 xen thân hai chữ số ấy thì được một số trong những mới lớn hơn số ban đầu 200 1-1 vị. Tìm kiếm số thuở đầu ?
Bài giải:
Gọi chữ số hàng trăm là: $x$ (với $xin mathbbN^*;,,00$)
Số gạo bán được trong ngày thứ hai là: $x-420$(kg)
Nếu ngày thứ nhất bán được thêm 120kg thì sẽ bán được số ki-lô-gam gạo là: $x+120$ (kg)
Theo đề bài ta có:$x+120=frac32left( x-420 ight)$
$Leftrightarrow x=1500$ (TM)
Vậy ngày thiết bị nhất shop bán được 1500 kilogam gạo.
Bài 6.
Tổng số dầu của hai thùng A và B là 125 lít. Nếu như lấy sút ở thùng dầu A đi 30 lít và cấp dưỡng thùng dầu B 10 lít thì số dầu thùng A bằng $frac34$số dầu thùng B. Tính số dầu lúc đầu ở mỗi thùng.
Bài giải
Gọi số dầu thuở đầu ở thùng A là: $x$ (lít) (với $00$ )
Chiều lâu năm của hình chữ nhật ban sơ là: $frac54x$ (cm)
Nếu tăng chiều dài thêm 3cm thì chiều hình chữ nhật lúc đó là: $frac54x+3$ (cm)
Nếu tăng chiều rộng thêm 8cm thì chiều rộng hình chữ nhật lúc đó là: $x+8$ (cm)
Theo bài bác ra ta có: $frac54x+3=x+8$
$Leftrightarrow frac14x=5$
$Leftrightarrow x=20$(TM)
Vậy chiểu rộng hình chữ nhật ban đầu là 20cm.
Chiều lâu năm hình chữ nhật lúc đầu là: $frac54.20=25$cm
Diện tích hình chữ nhật thuở đầu là: 20.25 = 500$cm^2$
Bài 11.
Một miếng khu đất hình chữ nhật có chu vi bởi 98m. Nếu sút chiều rộng lớn 5m cùng tăng chiều nhiều năm 2m thì diện tích giảm 101 $m^2$. Tính diện tích mảnh đất thuở đầu ?
Bài giải:
Tổng chiều dài cùng chiều rộng lớn của miếng khu đất hình chữ nhật là: 98 : 2 = 49 (m)
Gọi chiều rộng của miếng đất hình chữ nhật thuở đầu là: $x$ (m) (với $0 Bài giải
Đổi: 4 giờ đồng hồ 8 phút = $frac6215$ giờ; 40 phút = $frac23$ giờ
Gọi quãng con đường AB là $x$ (km) ($x>0$ )
Thời gian xe hơi đi từ bỏ A mang đến B là: $fracx35$ (giờ)
Thời gian xe hơi đi trường đoản cú B đến A là: $fracx30$ (giờ)
Tổng thời hạn cả đi lẫn về (không kể thời gian nghỉ là:$frac6215-frac23=frac5215$ (giờ)
Theo bài xích ra, ta có phương trình:
$fracx35+fracx30=frac5215$
$Leftrightarrow frac13x210=frac5215$
$Leftrightarrow x=56$ (thỏa mãn)
Vậy quãng con đường AB là 56 km.
Bài 14. Xem thêm: Tải Hình Chế Hài Hước Trên Facebook, Ảnh Chế Vui Về 'Chém Gió'
Một tín đồ đi xe hơi từ A cho B với tốc độ 40 km/h rồi trở lại A với tốc độ 36 km/h. Tính quãng đường AB, biết thời hạn đi từ bỏ A cho B ít hơn thời hạn đi từ B về A là 10 phút.
Bài giải
Đổi: 10 phút = $frac16$ giờ
Gọi quãng con đường AB là $x$ (km) ($x>0$ )
Thời gian xe hơi đi từ bỏ A mang đến B là: $fracx40$ (giờ)
Thời gian ô tô đi từ bỏ B đến A là: $fracx36$ (giờ)
Theo bài xích ra, ta có phương trình:
$fracx36-fracx40=frac16$
$Leftrightarrow fracx360=frac16$
$Leftrightarrow x=60$ (thỏa mãn)
Vậy quãng mặt đường AB là 60 km.
Bài 15.
Một ô tô đi từ A cho B với tốc độ 40 km/h. Trên quãng mặt đường từ B về A, gia tốc ô tô tăng lên 10 km/h nên thời hạn về ngắn lại hơn thời gian đi là 36 phút. Tính quãng con đường từ A mang đến B?
Bài giải
Đổi: 36 phút = $frac35$ giờ
Gọi quãng con đường AB là $x$ (km) ($x>0$ )
Thời gian xe hơi đi từ bỏ A cho B là: $fracx40$ (giờ)
Vận tốc ô tô đi trường đoản cú B về A là: 40 + 10 = 50 (km/h)
Thời gian ô tô đi tự B đến A là: $fracx50$ (giờ)
Theo bài xích ra, ta gồm phương trình:
$fracx40-fracx50=frac35$
$Leftrightarrow fracx200=frac35$
$Leftrightarrow x=120$ (thỏa mãn)
Vậy quãng đường AB là 120 km.
Câu 16:
Một xe cộ ô tô dự định đi tự A mang đến B với tốc độ 48 km/h. Sau khi đi được một giờ thì xe pháo bị lỗi phải dừng lại sửa 15 phút. Cho nên vì thế đến B đúng giờ ý định ô tô yêu cầu tăng tốc độ thêm 6 km/h. Tính quãng đường AB ?
Bài giải:
Đổi: 15 phút = $frac14$ giờ
Gọi thời gian ô tô ý định đi trường đoản cú A đến B là: x (giờ) (x > 0)
Quãng đường ô tô đi được trong một giờ đầu là: 48. 1 = 48 (km)
Ô tô nên tăng gia tốc thêm 6 km/h nên tốc độ mới của xe hơi là:
48 + 6 = 54 (km/h)
Thời gian ô tô đi với gia tốc 54 km/h là:
x – 1 - $frac14$= x - $frac54$ (giờ)
Theo bài xích ra ta gồm phương trình:
$48x=48+54left( x-frac54 ight)$
$Leftrightarrow$ 48x = 48 + 54x - $frac1352$
$Leftrightarrow$$-6x=-frac392$
$Leftrightarrow x=frac134$
Vậy quãng con đường AB là: $frac134.48=156$ (km)
Câu 17:
Một xe hơi phải đi quãng mặt đường AB dài 60 km trong một thời hạn nhất định. Xe đi nửa đầu quãng con đường với vận tốc hơn dự tính 10 km/h với đi nửa sau kém hơn dự định 6 km/h. Biết ô tô đến đúng dự định. Tính thời hạn dự định đi quãng mặt đường AB ?
Bài giải:
Gọi vận tốc ô tô dự định đi quãng đường AB là: x (km/h) (x > 6)
Xe đi nửa quãng đường đầu với gia tốc là: x + 10 (km/h)
Xe đi nửa quãng mặt đường sau với tốc độ là: x – 6 (km/h)
Theo bài xích ra ta có:
$frac60x=frac30x+10+frac30x-6$
$Leftrightarrow frac60(x+10)(x-6)x(x+10)(x-6)=frac30x(x-6)(x+10)x(x-6)+frac30x(x+10)(x-6)x(x+10)$
$Rightarrow$ 60(x + 10)(x – 6) = 30x(x – 6) + 30x(x + 10)
$Leftrightarrow$ 2(x + 10)(x – 6) = x(x – 6) + x(x + 10)
$Leftrightarrow$$2x^2+8x-120=x^2-6x+x^2+10x$
$Leftrightarrow$ 4x = 120
$Leftrightarrow$x = 30 (thỏa mãn)
Vậy thời hạn dự định đi quãng mặt đường AB là: 60 : 30 = 2 (giờ)
Câu 18:
Một ô tô dự định đi từ A mang lại B với vận tốc 50km/h. Sau khi đi được $frac23$ quãng mặt đường với tốc độ đó, vì chưng đường khó khăn đi nên người lái xe xe phải giảm vận tốc mỗi giờ đồng hồ 10 km bên trên quãng con đường còn lại. Vày đó, tín đồ đó mang đến B chậm 1/2 tiếng so với dự định. Tính quãng mặt đường AB ?
Bài giải:
Đổi: trong vòng 30 phút = $frac12$ giờ
Gọi quãng đường AB là: x (km) (x > 0)
Thời gian dự tính ô tô đi là: $fracx50$ (giờ)
Thời gian để ô tô đi $frac23$ quãng đường với gia tốc 50 km/h là: $frac2x3.50=fracx75$ (giờ)
Thời gian để xe hơi đi $frac13$ quãng đường sót lại với vận tốc 40 km/h là: $fracx3.40=fracx120$ (giờ)
Theo bài bác ra ta gồm phương trình:
$fracx50=fracx75+fracx120-frac12$
$Leftrightarrow fracx50-fracx75-fracx120=-frac12$
$Leftrightarrow x.left( frac150-frac175-frac1120 ight)=-frac12$
$Leftrightarrow -frac1600x=-frac12$
$Leftrightarrow$ x = 300 (thỏa mãn)
Vậy quãng mặt đường AB dài là: 300 km
Bài 19:
Một ô tô đi từ tp hà nội đến Đền Hùng với vận tốc 30 km/h. Bên trên quãng con đường từ đền rồng Hùng về Hà Nội, tốc độ ô tô tăng thêm 10 km/h nên thời hạn về ngắn hơn thời gian đi là 30 phút. Tính quãng con đường tử tp hà nội đến Đền Hùng?
Bài giải:
Đổi: nửa tiếng = $frac12$ giờ
Gọi quãng mặt đường từ tp. Hà nội đến Đền Hùng là $x$ (km) $left( x>0 ight)$
Thời gian ô tô đi từ hà nội đến Đền Hùng là: $fracx30$ (giờ)
Vận tốc xe hơi từ Đền Hùng về thủ đô hà nội là: $30+10=40$ (km/h)
Thời gian ô tô từ Đền Hùng về hà thành là: $fracx40$ (giờ)
Theo bài ra, ta có:
$fracx30-fracx40=frac12$
$Leftrightarrow fracx120=frac12$
$Leftrightarrow x=60$ (thỏa mãn)
Vậy quãng con đường từ thành phố hà nội đến Đền Hùng là 60 (km)
Bài 20:
Một người đi xe máy ý định từ A mang đến B trong thời gian nhất định. Sau khi đi được nửa quãng con đường với vận tốc 30 km/h thì tín đồ đó đi tiếp nửa quãng đường còn lại với gia tốc 36 km/h cho nên đến B nhanh chóng hơn ý định 10 phút. Tính thời hạn dự định đi quãng mặt đường AB ?
Bài giải:
Đổi 10 phút = $frac16$ giờ
Gọi S là độ dài quãng con đường AB (km, S>0)
Thời gian tín đồ đó đi nửa quãng mặt đường đầu là: $fracS2.30$ giờ
Thời gian người đó đi nửa quãng mặt đường sau là: $fracS2.36$ giờ
Tổng thời hạn người đó đi quãng đường là: $fracS2.30+fracS2.36$ giờ
Thời gian bạn đó dự tính đi không còn quãng con đường đó là:
$fracS30$ giờ
Khi kia ta bao gồm phương trình:
$fracS2.30+fracS2.36=fracS30-frac16$
$Leftrightarrow S.left( frac160+frac172-frac130 ight)=-frac16$
Các em học viên đã học tập chương bất đẳng thức cùng bất phương trình sinh sống đầu công tác đại số học tập kì II lớp 10. Tuy nhiên, những học sinh gặp gỡ khó khăn khi giải bất phương trình vì không tính bất phương trình hàng đầu và bất phương trình bậc nhị còn có rất nhiều bất phương trình chứa bao gồm chứa căn thức với trị giỏi đối. Bởi đó, nhanlucnhanvan.edu.vn đã tổng hợp các công thức giải bất phương trình lớp 10, các em hoàn toàn có thể vận dụng để giải những bất phương trình từ dễ đến khó.
Mục Lục
2. Giải bất phương trình bậc nhất7. Bài bác tập bất phương trình gồm lời giải7.2 bài tập có lời giải bất phương trình bậc 21. Có mang bất phương trình
Bất phương trình một ẩn là 1 mệnh đề ( hay điện thoại tư vấn là biểu thức) tất cả chứa đổi mới x so sánh nhì hàm số f(x) và g(x) bên trên trường số thực dưới một trong những dạng: f(x)g(x),f(x)≤g(x),f(x)≥g(x).
Giao của nhì tập xác minh của các hàm số f(x) và g(x) thì được hotline là tập xác minh của bất phương trình.
2. Giải bất phương trình bậc nhất
2.1 bí quyết giải cùng biện luận bất phương trình số 1 một ẩn ax + b
* Trường phù hợp a # 0:
Ta hoàn toàn có thể sử dụng bảng xét vệt của nhị thức bậc nhất
Như vậy:
– Nếu a > 0, tập nghiệm là:
– Nếu a
* Trường đúng theo a = 0
Theo như bảng trên, tế bào tả bởi lời:
– Nếu b > 0, Phương trình rất nhiều nghiệm.
– Nếu b 2.2 Giải bất phương trình tích
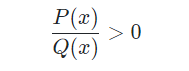
Trong đó, P(x) và Q(x) là rất nhiều nhị thức bậc nhất.
Cách giải: các em hãy lập bảng xét lốt của của P(x)/Q(x). Rồi tiếp nối suy ra được tập nghiệm của bất phương trình. Để đảm bảo tính đúng đắn của phép chia, những em tránh việc quy đồng với khử mẫu.
2.4 Giải bất phương trình bao gồm chứa tham số
Giải bất phương trình chứa tham số (m+a)x + b > 0 có nghĩa là xem xét rằng với các giá trị làm sao của tham số thì bất phương trình đang vô nghiệm hoặc có nghiệm và tìm ra các nghiệm đó.
Cách giải: phụ thuộc vào yêu ước đề, lập bảng xét dấu, biện luận tìm tham số m cân xứng và tra cứu nghiệm (nếu có).
3. Giải pháp giải bất phương trình bậc 2 một ẩn
Là BPT dạng: a.x2 + b.x + c > 0 cùng với a # 0
Đặt Δ = b2 − 4.a.c. Ta có những trường thích hợp sau:
Nếu Δ– a 0 thì BPT nghiệm đúng với đa số giá trị thực của x. Tập nghiệm là: R.
Nếu Δ = 0:– a 0 thì BPT nghiệm đúng với mọi giá trị thực của x. Tập nghiệm là:
Nếu Δ > 0, gọi x1, x2 (x1Khi đó:
– Nếu a > 0 thì tập nghiệm là: (−∞;x1)∪(x2;+∞)
– Nếu a Bảng xét dấu
Nhận xét:
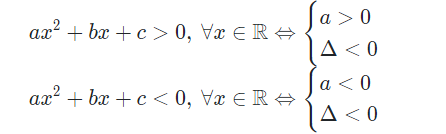
4. Giải bất phương trình đựng dấu quý hiếm tuyệt đối
Ta áp dụng định nghĩa và đặc thù của giá chỉ trị hoàn hảo nhất để khử dấu giá trị tuyệt đối hoàn hảo của bất phương trình:
Dạng 1:
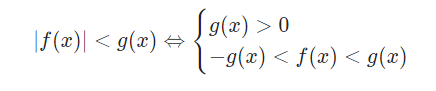
Dạng 2:
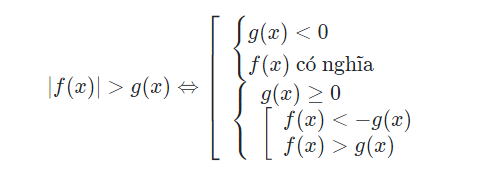
5. Giải bất phương trình cất căn thức
Để có thể khử căn thức và giải được dạng bài xích tập này, những em cần kết hợp phép nâng lũy vượt hoặc có thể đặt ẩn phụ.
6. Bài tập về bất phương trình
Bài 1/ BPT bậc nhất
1.1. Giải những bất phương trình sau:
1.2. Giải những bất phương trình sau:
1.3. Giải những bất phương trình sau:
Bài 2/ BPT qui về bậc nhất
Giải những bất phương trình sau:
Bài 3/ BPT bậc hai
Bài 4/ BPT qui về bậc hai gồm chứa vệt GTTĐ
Giải những bất phương trình sau:
Bài 5/ BPT qui về bậc hai bao gồm chứa căn thức
Giải những phương trình sau:
7. Bài xích tập bất phương trình tất cả lời giải
7.1 bài xích tập có lời giải bất phương trình bậc nhất
Bài 1:
Giải bất phương trình – 4x – 8 8: (- 4) ⇔ x > -2
Vậy tập nghiệm của bất phương trình -4x – 8 -2}
Biểu diễn bên trên trục số
Bài 2: Giải bất phương trình -0,2x – 0,2 > 0,4x – 2.
Gợi ý giải
-0,2x – 0,2 > 0,4x – 2
⇔ 0,4x – 2 0,4x – 2 là {x|x 3
b) x – 2x -4x + 2
d) 8x + 2 3
⇔ x > 3 + 5 (chuyển -5 từ vế trái sang vế đề nghị và đổi lốt thành 5)
⇔ x > 8.
Vậy nghiệm của bất phương trình là x > 8.
b) x – 2x -4x + 2
⇔ -3x + 4x > 2
⇔ x > 2
Vậy nghiệm của bất phương trình là x > 2.
d) 8x + 2 7.2 bài xích tập có giải mã bất phương trình bậc 2Dạng 1: Xét dấu của tam thức bậc 2
* lấy một ví dụ 1 (Bài 1 trang 105 SGK Đại Số 10): Xét dấu những tam thức bậc hai:
a) 5×2 – 3x + 1
b) -2×2 + 3x + 5
c) x2 + 12x + 36
d) (2x – 3)(x + 5)
Lời giải lấy ví dụ 1 (Bài 1 trang 105 SGK Đại Số 10):
a) 5×2 – 3x + 1
– Xét tam thức f(x) = 5×2 – 3x + 1
– Ta có: Δ = b2 – 4ac = 9 – 20 = –11 0 ⇒ f(x) > 0 với ∀ x ∈ R.
b) -2×2 + 3x + 5
– Xét tam thức f(x) = –2×2 + 3x + 5
– Ta có: Δ = b2 – 4ac = 9 + 40 = 49 > 0.
– Tam thức bao gồm hai nghiệm phân biệt x1 = –1; x2 = 5/2, hệ số a = –2
f(x) > 0 lúc x ∈ (–1; 5/2)- từ bỏ bảng xét dấu ta có:
f(x) = 0 khi x = –1 ; x = 5/2
f(x) 0.
– Ta bao gồm bảng xét dấu:
– tự bảng xét lốt ta có:
f(x) > 0 với ∀x ≠ –6
f(x) = 0 khi x = –6
d) (2x – 3)(x + 5)
– Xét tam thức f(x) = 2×2 + 7x – 15
– Ta có: Δ = b2 – 4ac = 49 + 120 = 169 > 0.
– Tam thức có nhì nghiệm phân biệt x1 = 3/2; x2 = –5, thông số a = 2 > 0.
– Ta tất cả bảng xét dấu:
– tự bảng xét lốt ta có:
f(x) > 0 lúc x ∈ (–∞; –5) ∪ (3/2; +∞)
f(x) = 0 khi x = –5 ; x = 3/2
f(x) Dạng 2: Giải những bất phương trình bậc 2 một ẩn
* lấy một ví dụ 1 (Bài 3 trang 105 SGK Đại Số 10): Giải các bất phương trình sau
a) 4×2 – x + 1
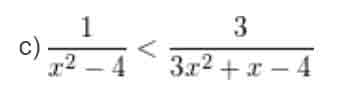
d) x2 – x – 6 ≤ 0
° giải mã ví dụ 1 (bài 3 trang 105 SGK Đại Số 10):
a) 4×2 – x + 1 0 phải f(x) > 0 ∀x ∈ R
⇒ Bất phương trình đã mang đến vô nghiệm.
b) -3×2 + x + 4 ≥ 0
– Xét tam thức f(x) = -3×2 + x + 4
– Ta gồm : Δ = 1 + 48 = 49 > 0 gồm hai nghiệm x = -1 cùng x = 4/3, hệ số a = -3
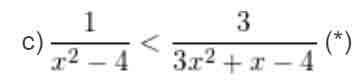
– Điều khiếu nại xác định: x2 – 4 ≠ 0 với 3×2 + x – 4 ≠ 0
⇔ x ≠ ±2 với x ≠ 1; x ≠ 4/3.
– đưa vế và quy đồng mẫu tầm thường ta được:
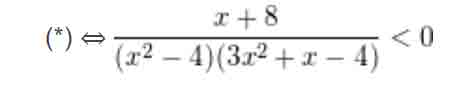
– Nhị thức x + 8 gồm nghiệm x = -8
– Tam thức x2 – 4 gồm hai nghiệm x = 2 cùng x = -2, hệ số a = 1 > 0
⇒ x2 – 4 mang dấu + khi x 2 và có dấu – khi -2 0.
⇒ 3×2 + x – 4 mang dấu + lúc x 1 có dấu – khi -4/3
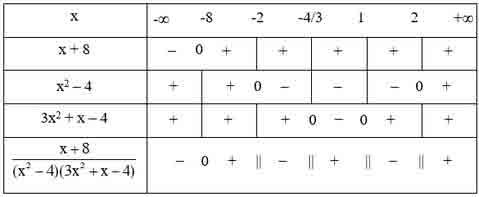
– từ bỏ bảng xét lốt ta có:
(*) 0
⇒ f(x) ≤ 0 lúc -2 ≤ x ≤ 3.
⇒ Tập nghiệm của bất phương trình là: S = <-2; 3>.
Dạng 3: xác minh tham số m thỏa đk phương trình* ví dụ như 1 (Bài 4 trang 105 SGK Đại Số 10): Tìm những giá trị của tham số m để các phương trình sau vô nghiệm
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0
b) (3 – m)x2 – 2(m + 3)x + m + 2 = 0
° giải mã ví dụ 1 (bài 4 trang 105 SGK Đại Số 10):
a) (m – 2)x2 + 2(2m – 3)x + 5m – 6 = 0 (*)
• ví như m – 2 = 0 ⇔ m = 2, lúc đó phương trình (*) trở thành:
2x + 4 = 0 ⇔ x = -2 tuyệt phương trình (*) gồm một nghiệm
⇒ m = 2 chưa phải là giá trị phải tìm.
• Nếu m – 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ’ = b’2 – ac = (2m – 3)2 – (m – 2)(5m – 6)
= 4m2 – 12m + 9 – 5m2 + 6m + 10m – 12
= -m2 + 4m – 3 = (-m + 3)(m – 1)














